摘 要： 針對目前汽車開閉件開發(fā)周期較長和運動分析精度不足等問題, 通過Matlab建立了某車型雜物盒鉸鏈的運動學方程, 求解出鉸鏈機構(gòu)中彈簧的運動曲線。同時, 采用機械系統(tǒng)動力學軟件Adams建立了機構(gòu)運動模型, 并對設(shè)計階段中雜物盒的操作力和位移等動力學特性進行了仿真分析, 驗證了兩種分析方法具有很好的一致性, 從而提高了求解效率, 也為鉸鏈機構(gòu)的優(yōu)化設(shè)計提供了理論基礎(chǔ)。

0 引言

隨著汽車產(chǎn)業(yè)和計算機技術(shù)的高速發(fā)展, 客戶對產(chǎn)品個性化定制的需求越來越高, 在滿足基本外觀和功能的同時, 汽車設(shè)計也呈現(xiàn)出多種研究趨[1]。在歐洲車展中, 汽車開閉件廣泛采用了六連桿鉸鏈機構(gòu), 該鉸鏈除了造型美觀、方便實現(xiàn)密封外, 還可通過改變各連桿的長度、鉸鏈點的位置以及彈簧系數(shù)等參數(shù), 從而實現(xiàn)對機構(gòu)運動學特性的控制[2]。

機構(gòu)運動學主要研究物體間的相對運動即位移、速度和加速度隨時間變化的關(guān)系。由于傳統(tǒng)的機構(gòu)運動學、動力學分析對于復雜的機械運動, 尤其汽車開閉件運動, 雖然能給出解析表達式, 但難以快速計算出滿足工程設(shè)計要求的精確結(jié)果[3-4]。

針對某車型雜物盒的鉸鏈模型, 通過模擬和計算人手開閉雜物盒的動作, 在Matlab中求解出鉸鏈彈簧的運動曲線[5]。同時, 采用虛擬樣機技術(shù)在Adams中建立幾何模型, 并設(shè)置各個運動學參數(shù), 進行仿真分析和驗證, 從而提高求解效率, 縮短產(chǎn)品研發(fā)周期[6]。

1 雜物盒鉸鏈機構(gòu)

如圖1所示, 汽車駕駛室內(nèi)部的雜物盒多采用鉸鏈式開啟機構(gòu), 該機構(gòu)由兩個彈簧和多個連桿組成, 其結(jié)構(gòu)設(shè)計簡單, 旋轉(zhuǎn)點和連桿長度一旦確定, 則盒蓋在任何一個開啟角度下的位置都是唯一的。鉸鏈連桿機構(gòu)的設(shè)計要求主要包括:

(1) 由于造型限制, 盒蓋的初始位置與面板配合關(guān)系滿足設(shè)計要求。

(2) 開啟角度必須方便車內(nèi)乘員取放物品, 不能與其他結(jié)構(gòu)干涉。

(3) 雜物盒開啟、關(guān)閉操作輕便, 盒蓋位于最大開啟角度位置時, 能可靠鎖止, 如圖2所示。

圖1 某車型盒蓋開閉狀態(tài)

圖2 盒蓋開啟示意圖

雜物盒的最大開度主要由彈簧的行程決定, 因此通過計算兩個鉸鏈彈簧在拉伸和壓縮過程中的位移和作用力變化, 從而得出該鉸鏈機構(gòu)的運動規(guī)律, 如圖3所示。

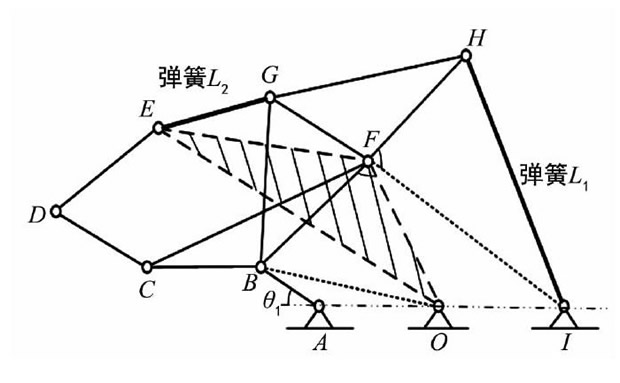
如圖4所示, 該鉸鏈機構(gòu)的連桿長度共有15處, 各旋轉(zhuǎn)點的位置關(guān)系也隨雜物盒的開啟而變化。其中, AO、OI為定桿 (固定在面板上) , EG和HI為彈簧, CD為輸出件 (固定在盒蓋上) , BCF、BFG、FGH和EOF為三角構(gòu)件。

圖3 鉸鏈機構(gòu)模型

圖4 鉸鏈六桿機構(gòu)

由于彈簧EG和HI長度可變, 因此不夠成約束, 先忽略彈簧連桿機構(gòu)。如圖5所示, 該連桿之間采用旋轉(zhuǎn)副連接, 盒蓋的開啟和關(guān)閉運動是旋轉(zhuǎn)和平移的結(jié)合。可以看出, 該機構(gòu)有唯一的運動軌跡[7]。

圖5 簡化的鉸鏈六桿機構(gòu)

2 Matlab數(shù)值計算

2.1 鉸鏈四連桿機構(gòu)

鉸鏈連桿機構(gòu)結(jié)構(gòu)簡單、制造容易、可承載較大載荷、方便實現(xiàn)已知的運動規(guī)律和再現(xiàn)已知的運動軌跡, 因此廣泛應用在工程設(shè)計中[8-10]。鉸鏈四連桿機構(gòu)可通過改變構(gòu)件形狀和尺寸, 取不同構(gòu)件為機架, 運動副逆換和擴大轉(zhuǎn)動副等方法, 將鉸鏈四連桿機構(gòu)演化為多種連桿機構(gòu)[11]。

如圖6所示, 在直角坐標系中, 以封閉的矢量多邊形ABFO為例, 建立位置方程[12]。

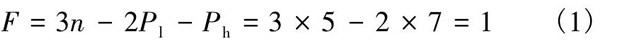
將矢量形式轉(zhuǎn)為復數(shù)形式, 則:

由歐拉公式e=cosθ+isinθ將式 (2) 實部與虛部分離, 則:

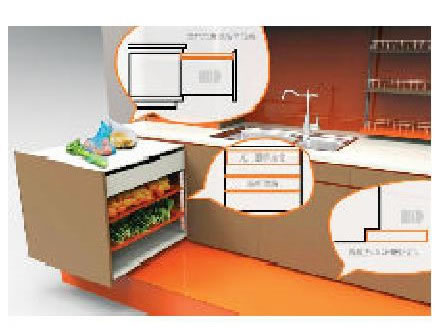
圖6 鉸鏈四連桿機構(gòu)

2.1 鉸鏈彈簧L1的運動分析

如圖7所示, 將該機構(gòu)分解成兩個四連桿機構(gòu), 并通過解析法求解鉸鏈彈簧L1的運動規(guī)律。

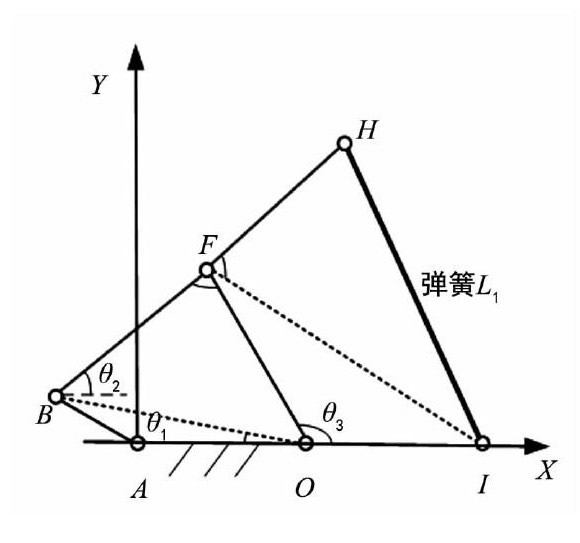
圖7 鉸鏈六連桿機構(gòu)

在三角形△FIH中, 彈簧L1的長度變化即HI的位移變化, 計算出彈簧L1=HI的長度為:

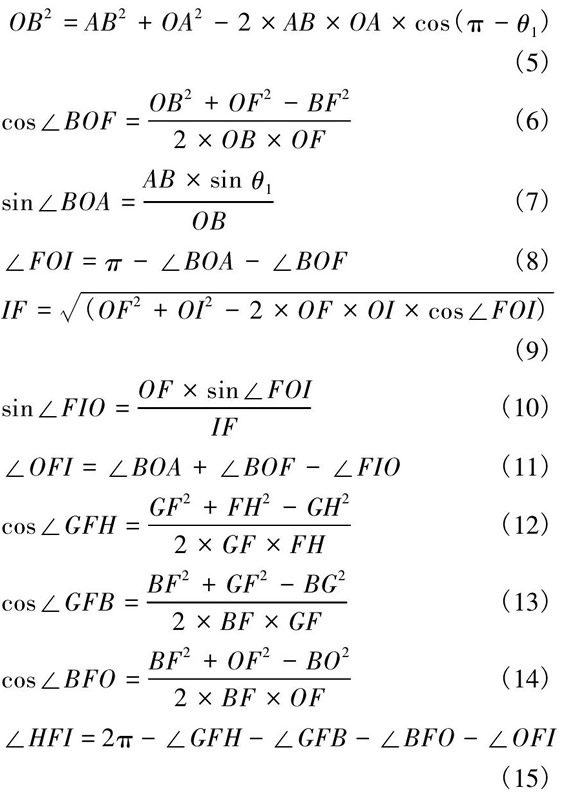
運行Matlab程序, 得出盒蓋在關(guān)閉過程中, 鉸鏈彈簧L1的運動曲線, 如圖8所示。

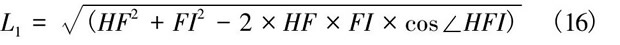
圖8 彈簧L₁時間-位移圖

2.2 彈簧L₂的運動分析

如圖9所示, 同樣將該機構(gòu)分解成兩個四連桿機構(gòu), 并通過解析法求解鉸鏈彈簧L₂的運動規(guī)律。

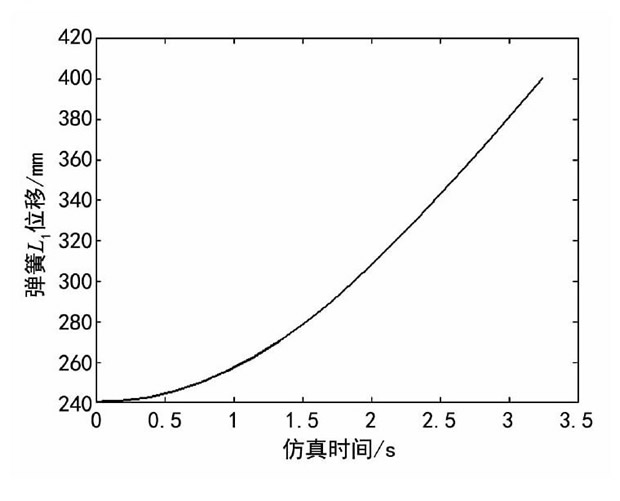
圖9 鉸鏈六連桿機構(gòu)

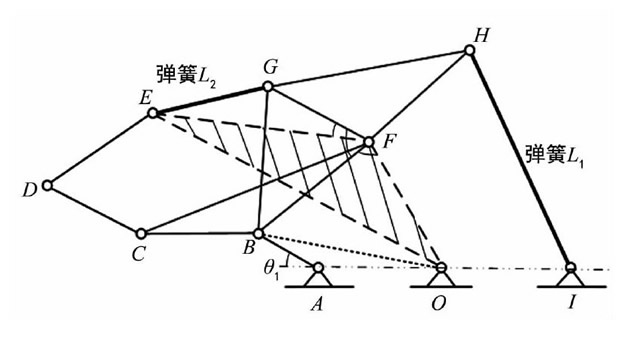
在三角形△EFG中, 彈簧L₂的長度變化即EG的位移變化, 計算出彈簧L₂=EG的長度為:

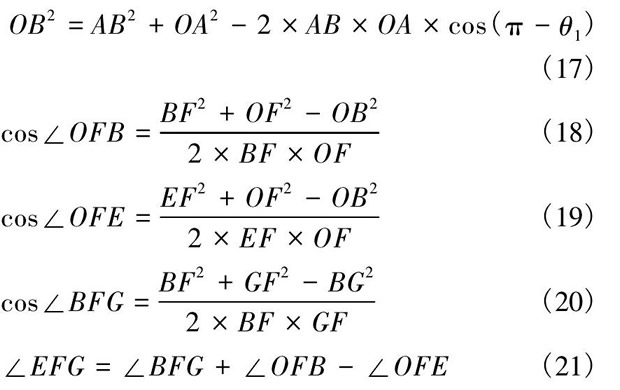
運行Matlab程序, 得出得出盒蓋在關(guān)閉過程中, 鉸鏈彈簧L₂的運動曲線, 如圖10所示。 分析發(fā)現(xiàn), 隨著關(guān)閉時間的增大, 彈簧L₂的位移逐漸減小, 在最小值時, 彈簧位移達到最小值。隨后彈簧L2的又迅速增大, 且位移最小值的坐標為 (t0, Lmin) = (1.93, 213.8) 。

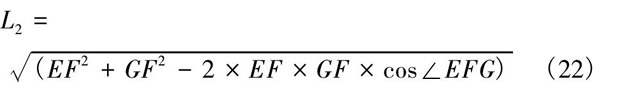
圖10 彈簧L2時間-位移圖

3 Adams仿真分析

3.1 鉸鏈彈簧模型建立

如圖11所示, 在Adams中建立鉸鏈六連桿彈簧仿真模型, 并添加約束和驅(qū)動力, 從而得出兩個彈簧的位移、速度和加速度曲線。設(shè)定鉸鏈連桿AB以定角速度順時針轉(zhuǎn)動, 轉(zhuǎn)動副的驅(qū)動函數(shù)為30.0 d*time, 即角速度30°/s。

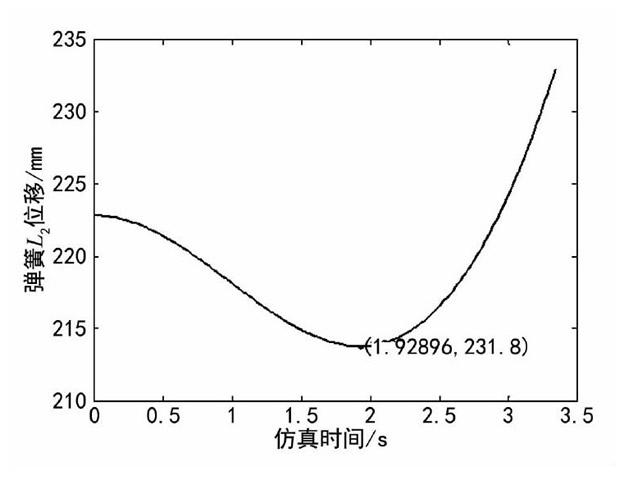
圖11 鉸鏈彈簧仿真模型

通過分析鉸鏈彈簧的特性, 計算出彈簧在拉伸和壓縮過程中的行程和作用力曲線圖。分別設(shè)定4個測量值:鉸鏈彈簧的長度MEA_PT2PT_length、運動速度MEA_PT2PT_velocity、鉸鏈彈簧的加速度MEA_PT2PT_acceleration和鉸鏈彈簧的作用力MEA_PT2PT_force。

根據(jù)彈簧運動速度MEA_PT2PT_velocity的測量值為正為負, 可以判斷該彈簧處于壓縮狀態(tài)還是拉伸狀態(tài);而根據(jù)長度MEA_PT2PT_length的測量值, 可以判斷彈簧的壓縮量和拉伸量。

3.2 鉸鏈彈簧仿真分析

設(shè)置仿真時間3.4 s, 步數(shù)為100步, 開始仿真。進入后處理模塊Adams/Post Processor, 得到鉸鏈彈簧L1的運動曲線, 分別如圖12和圖13所示。

通過Adams仿真分析, 彈簧L1的長度和作用力變化曲線如圖12所示。在關(guān)閉雜物盒過程中, 鉸鏈彈簧的速度為正, 說明彈簧L1處于拉伸狀態(tài)。

由胡克定律F=-kx可知, 彈簧力方向與拉伸量方向相反, 彈簧力F1的仿真結(jié)果如圖13所示。隨著盒蓋的關(guān)閉, 彈簧的拉伸量逐漸增大, 說明關(guān)閉盒蓋作用力也是逐漸增大。

圖12 彈簧L₁速度和加速度曲線

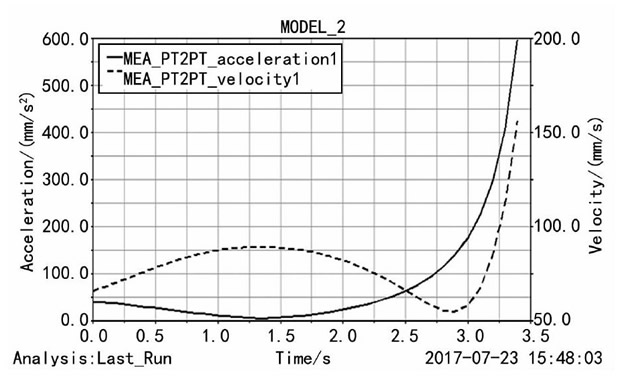
圖13 彈簧L₁位移和作用力曲線

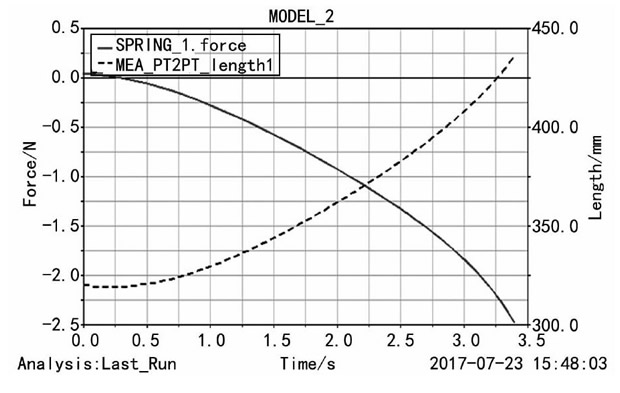
圖14 彈簧L₂速度和加速度曲線

如圖14所示, 在盒蓋開始關(guān)閉過程中, 彈簧L2的速度慢慢大, 通過最高點后, 速度迅速變小, 最后達到關(guān)閉雜物盒的極限狀態(tài), 此時速度為0, 說明在關(guān)閉雜物盒過程中, 鉸鏈彈簧L₂速度為正, 且一直處于拉伸狀態(tài)。盒蓋關(guān)閉速度先增大后變小直至為0, 從而避免因關(guān)閉速度過大產(chǎn)生較大響聲, 提高了雜物盒的操作耐久性。

如圖15所示, 在關(guān)閉雜物盒過程中, 彈簧L2的作用力MEA_PT2PT_force2慢慢變大, 在通過最大值后, 作用力逐漸減小直至為0, 然后又反向迅速增大直至關(guān)閉狀態(tài)。

圖15 彈簧L₂位移和作用力曲線

因此, 在分析雜物盒開啟的運動過程可知, 彈簧L2在開始階段壓縮量變化很大, 因此需要較大的力才能開啟;在通過最大值之后, 壓縮量變化不大, 只需很小力就很容易地達到開啟狀態(tài)。

3.3 仿真結(jié)果對比分析

為了方便對比鉸鏈彈簧L₂的誤差大小, 設(shè)定9組不同的仿真時間, 分別將Matlab和Adams分析的位移曲線數(shù)據(jù)導出, 進行對比分析, 結(jié)果如圖16所示, 仿真結(jié)果對比如表1所列。

表1 仿真結(jié)果對比

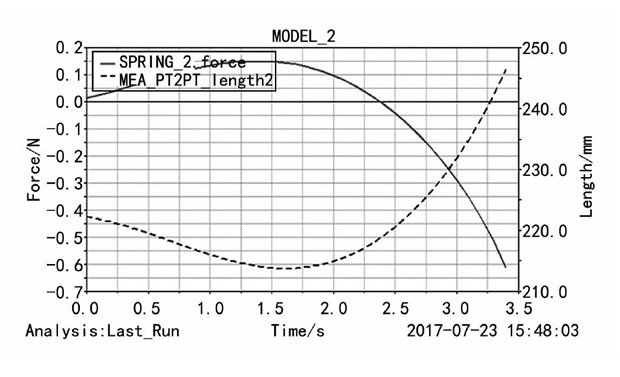
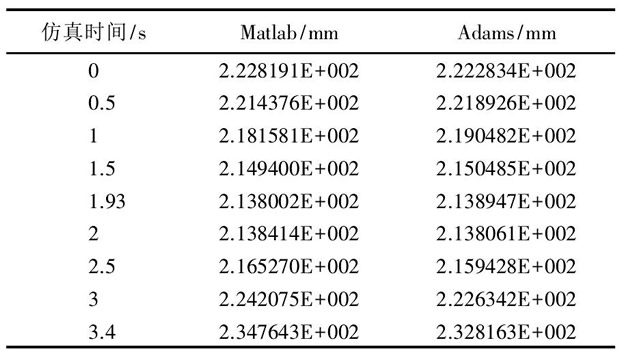
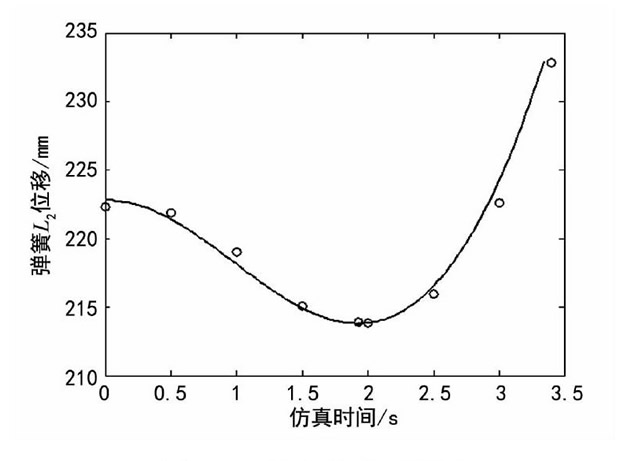
圖16 時間-位移對比圖

將表1中各組數(shù)據(jù)進行對比, 發(fā)現(xiàn)兩種方法的數(shù)值相差較小, 取其中最大的一組 (第9組) 進行計算。

結(jié)果表明, Matlab解析法和Adams仿真法得到的分析結(jié)果相差不大, 最大相對誤差不超過0.84%, 兩種方法具有很好的一致性。

4 結(jié)語

(1) 建立了鉸鏈彈簧機構(gòu)的運動學方程, 并進行了建模仿真, 分析了鉸鏈彈簧的運動規(guī)律, 驗證了兩種方法的可行性和一致性。

(2) Matlab解析法處理數(shù)據(jù)更加多元, 而Adams建模仿真更加簡便, 大大提高了求解效率。

(3) Matlab解析法和Adams仿真法兩者之間的演算便于計算的準確性, 為鉸鏈機構(gòu)的優(yōu)化設(shè)計提供了理論基礎(chǔ)。

參考文獻

[1]朱建文, 周波, 孟正大.基于Adams的150 kg機器人運動學分析及仿真[J].工業(yè)控制計算機, 2017 (7) :82-84.

[2]單長洲, 王火文, 陳超.基于ADAMS的某重型卡車駕駛室懸置振動模態(tài)分析[J].汽車實用技術(shù), 2017 (12) :233-236.

[3]Hamza K.Multi-objective design of vehicle suspension systems via a local diffusion genetic algorithm for disjoint Pareto frontiers[J].Engineering Optimization, 2015, 47 (5) :706-717.

[4]于海峰.基于ADAMS/Car的懸架系統(tǒng)對操縱穩(wěn)定性影響的仿真試驗研究[D].大連:大連理工大學, 2007.

[5]馬如奇, 郝雙暉, 鄭偉峰, 等.基于MATLAB與ADAMS的機械臂聯(lián)合仿真研究[J].機械設(shè)計與制造, 2010 (4) :93-95.

[6]王曉蓮.基于ADAMS和MATLAB的汽車主動懸架聯(lián)合仿真研究[D].長春:吉林大學, 2009.

[7]孫澤敏.基于ADAMS的某車懸架系統(tǒng)運動學仿真及優(yōu)化[D].長春:長春工業(yè)大學, 2014.

[8]郭銳, 褚超美.基于ADAMS抽油機的運動學仿真與優(yōu)化設(shè)計[J].電子科技, 2017 (7) :44-46+54.

[9]楊艷.基于輪式驅(qū)動的新能源載重汽車自適應巡航控制及仿真研究[D].成都:西南交通大學, 2017.

[10]桂軍.基于ADAMS的汽車行駛平順性仿真分析及優(yōu)化[D].錦州:遼寧工業(yè)大學, 2014.

[11]王戰(zhàn)中, 楊長建, 劉超穎, 等.基于MATLAB和ADAMS的六自由度機器人聯(lián)合仿真[J].制造業(yè)自動化, 2013 (18) :30-33.

[12]高露, 趙利, 周海君, 等.基于ADAMS的新型三臂輪式巡檢機器人運動學仿真[J].機械研究與應用, 2017, 30 (3) :5-7.

作者簡介：夏然飛 (1990-) , 男, 湖北武漢人, 碩士研究生, 研究方向:機械系統(tǒng)仿真、汽車設(shè)計。