摘要：零剛度柔性鉸鏈的轉動剛度近似為零，克服了普通柔性鉸鏈需要驅動力矩的缺陷，可應用于柔性夾持器等領域。以純 扭矩作用下的內外環(huán)柔性鉸鏈為正剛度子系統(tǒng)，研究負剛度機構并匹配正負剛度，可構造零剛度柔性鉸鏈。提出一種負剛度轉動機構——曲柄彈簧機構，建模分析了其負剛度特性；通過匹配正負剛度，分析了曲柄彈簧機構的結構參數(shù)對零剛度品質 的影響；提出一種可定制剛度和尺寸的線性彈簧——菱形片簧串，建立其剛度模型并進行了有限元仿真驗證；最終，完成了 一種結構緊湊的零剛度柔性鉸鏈樣件的設計、加工和測試。測試結果表明：純扭矩作用下，±18°轉角范圍內，零剛度柔性鉸鏈的轉動剛度比內外環(huán)柔性鉸鏈平均降低了93%。所構造的零剛度柔性鉸鏈結構緊湊，零剛度品質高；所提出的負剛度轉動 機構和可定制剛度的線性彈簧對柔性機構的研究具有較大的參考價值。

0 前言

柔性鉸鏈(軸承)^[1-2]依靠柔性單元的彈性變形 傳遞或轉化運動、力和能量，已廣泛應用于精密定位等領域。與傳統(tǒng)剛性軸承相比，柔性鉸鏈轉動時存在恢復力矩，因此，驅動單元需要提供輸出力矩 以驅動并保持柔性鉸鏈的轉動。零剛度柔性鉸鏈 ^[3](Zero stiffness flexural pivot, ZSFP)是一種轉動剛 度近似為零的柔性轉動關節(jié)。這類柔性鉸鏈可停留 在行程范圍內的任意位置，也稱為靜平衡柔性鉸鏈 ^[4]，多應用于柔性夾持器等領域。

基于柔性機構模塊化的設計理念，可將整個零剛度柔性鉸鏈系統(tǒng)分為正負剛度兩個子系統(tǒng)，通過 正負剛度的匹配實現(xiàn)零剛度系統(tǒng)^[5]。其中，正剛度子系統(tǒng)通常為大行程柔性鉸鏈，如交叉簧片柔性鉸鏈^[6-7]、廣義三交叉簧片柔性鉸鏈^[8-9]和內外環(huán)柔性 鉸鏈^[10-11]等。目前，柔性鉸鏈的研究已取得了較多成果，因此，設計零剛度柔性鉸鏈的關鍵在于：為柔性鉸鏈匹配合適的負剛度模塊[3]。

內外環(huán)柔性鉸鏈(Inner and outer ring flexural pivots, IORFP)在剛度、精度和溫漂等方面特性優(yōu) 良，三維模型如圖4。以純扭矩作用下的內外環(huán)柔性鉸鏈為正剛度子系統(tǒng)，通過研究相匹配的負剛度 模塊，給出零剛度柔性鉸鏈的構造方法，最終，完成零剛度柔性鉸鏈的設計、樣件加工和測試。

1 曲柄彈簧機構

1.1 負剛度的定義

剛度K 的一般定義是彈性元件所承受的載荷F與對應變形dx的變化率
K= dF/dx (1)
當彈性元件所受載荷增量與對應的變形增量符號相反時，即為負剛度。物理上，負剛度對應彈性元件的靜力不穩(wěn)定^[12]。負剛度機構在柔性靜平衡領域有著重要的作用。通常，負剛度機構具有以下特點。

(1) 機構儲備了一定能量或發(fā)生了一定形變。

(2) 機構處于臨界失穩(wěn)狀態(tài)。

(3) 機構受到微小擾動離開平衡位置時，可釋放出較大的力，并與運動方向相同。

1.2 零剛度柔性鉸鏈的構造原理

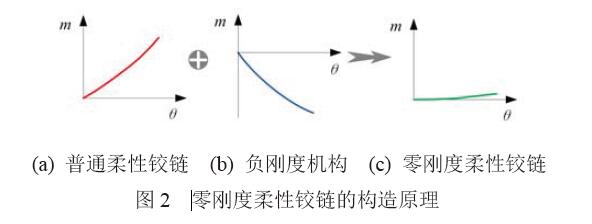
利用正負剛度匹配可構造零剛度柔性鉸鏈，原理如圖2 所示。

(1) 純扭矩作用下，內外環(huán)柔性鉸鏈具有近似線性的扭矩-轉角關系，如圖2a所示。特別地，當 交叉點位于簧片長度的12.73%時，其扭矩-轉角關系為線性^[11]，此時，柔性鉸鏈的恢復力矩Mpivot(順時針方向)與軸承轉角θ(逆時針方向)關系為
Mpivot=（8EI/L）θ (2)
式中，E 為材料彈性模量，L為簧片長度，I 為截面慣性矩。

(2) 根據(jù)內外環(huán)柔性鉸鏈的轉動剛度模型，匹配負剛度轉動機構，其負剛度特性如圖2b所示。

(3) 鑒于負剛度機構的不穩(wěn)定性^[12]，零剛度柔性鉸鏈的剛度應近似為零且大于零，如圖2c所示。

1.3 曲柄彈簧機構的定義

由文獻[4]，在柔性鉸鏈的運動剛體和固定剛體之間引入預變形彈簧，可以構造零剛度柔性鉸鏈。 對于圖1所示的內外環(huán)柔性鉸鏈，在內環(huán)和外環(huán)之間引入彈簧，即引入曲柄彈簧機構(Spring-crank mechanisms, SCM)。參照圖3 所示的曲柄滑塊機構， 曲柄彈簧機構相關參數(shù)如圖4所示。曲柄彈簧機構由曲柄和彈簧(設剛度為K)構成，初始角β為彈簧未變形時，曲柄AB 和基座AC之間的夾角；r表示曲柄長度，l表示基座長度，定義曲柄長度比ξ為r 與l的比值，即ξ=r/l(0<ξ<1)。

構造曲柄彈簧機構需要確定4個參數(shù)：基座長度l，曲柄長度比ξ，初始角β 和彈簧剛度K。

曲柄彈簧機構受力變形如圖5a所示，在力矩M_γ作用下，曲柄由初始位置AB_β轉動至AB_γ，轉動過程中，曲柄相對水平位置的夾角_γ 稱為曲柄轉角。

定性分析可得：曲柄從ABβ轉動(初始位置，Mγ 為零)至AB0(“死點”位置，M_γ為零)的過程中，曲柄彈簧機構存在一段具有負剛度特性的變形。

1.4 曲柄彈簧機構的力矩與轉角關系

圖5 中，取力矩Mγ順時針為正，曲柄轉角γ逆時針為正，下面建模分析力矩載荷M_γ與曲柄轉角_γ 之間的關系，建模過程是有量綱的。

如圖5b 所示，對曲柄ABγ列力矩平衡方程

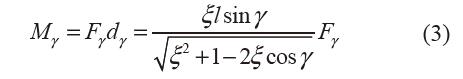
式中，F(xiàn)γ為彈簧恢復力，dγ為Fγ 對A點力臂。 假設彈簧的位移載荷關系為

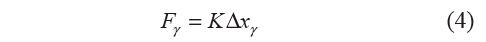
式中，K為彈簧剛度(不一定為常值)，Δ_xγ 為彈簧變 形量(縮短為正)，Δ_xγ=|B_βC| – |B_γC|。

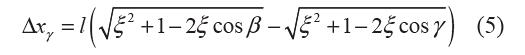
聯(lián)立式(3)～(5)，力矩M_γ 與轉角_γ的關系為

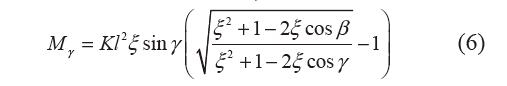
1.5 曲柄彈簧機構的負剛度特性分析

為便于分析曲柄彈簧機構的負剛度特性(力矩 M_γ 與轉角_γ 的關系)，不妨假設彈簧具有線性正剛 度，則式(4)可改寫為

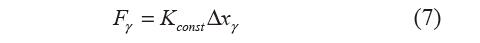
式中，Kconst 為大于零的常量。 柔性鉸鏈尺寸確定后，基座長度l也隨之確定， 因此，假設l 為常量。則式(6)可改寫為

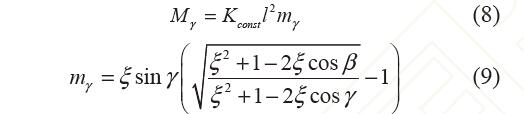
式中，Kconstl2 為大于零的常量，力矩系數(shù)mγ 的量綱 為一。分析力矩系數(shù)mγ與轉角γ的關系即可得到曲 柄彈簧機構的負剛度特性。

由式(9)，圖6 為初始角β=π 時，mγ 與曲柄長度比ξ和轉角γ 的關系，ξ∈[0.1, 0.9]，γ∈[0, π]。圖7為ξ=0.2 時，不同β 下，mγ 與轉角γ 的關系。圖8 為β=π 時，不同ξ 下，mγ 與轉角γ 的關系。

根據(jù)曲柄彈簧機構的定義(第1.3 節(jié))和式(9)， 當K和l為常量時，mγ 僅與轉角γ、曲柄長度比ξ和曲柄初始角β 有關。

(1) 當且僅當γ 等于0 或π 或β，mγ等于零；γ ∈[0, β]，mγ 大于零；γ∈[β，π]，mγ 小于零。 ∈[0, β]，mγ 大于零；γ∈[β，π]，mγ 小于零。

(2) γ∈[0, β]時，轉角γ 增大，mγ從零先增大， 至拐點角度γ0處取最大值mγmax，后又逐漸減小。

(3)曲柄彈簧機構的負剛度特性范圍：γ∈[0, γ0]， 此時γ 增大(逆時針方向)，力矩Mγ增大(順時針方 向)。拐點角度γ0 為曲柄彈簧機構負剛度特性最大轉 角且γ0∈[0, β]；mγmax 為最大負力矩系數(shù)。給定β 和ξ，對式(9)求導，可得γ0

(4) 初始角β越大，γ0 越大，m_γmax 越大。

(5) 長度比ξ越大，γ0 越小，m_γmax 越大。

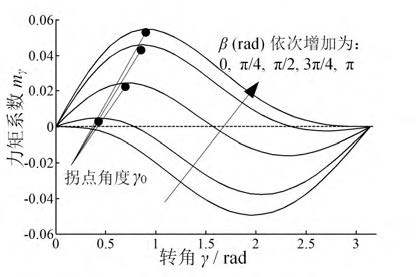
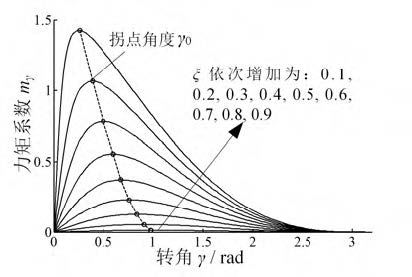
特別地，β=π時，曲柄彈簧機構負剛度特性最佳(負剛度轉角范圍大，能提供的力矩大)。β=π時，不同ξ條件下，曲柄彈簧機構負剛度特性最大 轉角γ0及最大負力矩系數(shù)mγmax 列于表1。

表1 初始角為π 時，不同曲柄長度比ξ 條件下的負剛度最大轉角γ0和最大力矩系數(shù)m_γmax

參數(shù)	數(shù)值
曲柄長度比 ξ	0.1	0.2	0.3	0.4	0.5
最大轉角 γ0/rad	0.98	0.91	0.84	0.76	0.68
最大力矩系數(shù)mγmax	0.013	0.055	0.13	0.23	0.37

 

2 零剛度柔性鉸鏈的構造

2.1 正負剛度的匹配如圖9所示，n(n≥2)組并聯(lián)的曲柄彈簧機構圓 周均布，構成與內外環(huán)柔性鉸鏈匹配的負剛度機構。

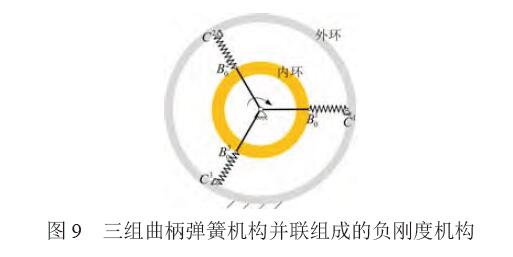
以內外環(huán)柔性鉸鏈為正剛度子系統(tǒng)，構造零剛度柔性鉸鏈。為實現(xiàn)零剛度，匹配正負剛度

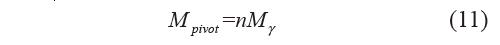
聯(lián)立式(2)、(3)、(6)、(11)，且γ=θ，可得彈簧的載荷Fγ 與位移Δxγ 的關系為

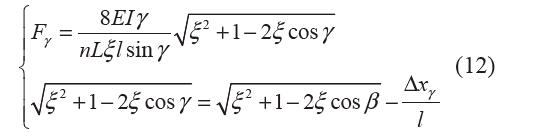
由第1.5 節(jié)，曲柄彈簧機構的負剛度轉角范圍： γ∈[0, γ0]且γ0∈[0, β]，則零剛度柔性鉸鏈的行程應小于γ0，即彈簧始終處于變形狀態(tài)(Δxγ≠0)。 內外環(huán)柔性鉸鏈的轉動范圍為±0.35 rad(±20°)， 對三角函數(shù)sinγ 和cosγ 做如下簡化

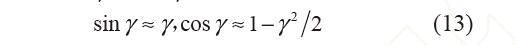
簡化后，彈簧的載荷-位移關系

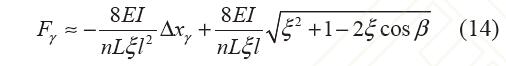
2.2 正負剛度匹配模型的誤差分析

評估式(13)的簡化處理所造成的誤差。根據(jù)零剛度柔性鉸鏈實際加工參數(shù)(第4.2 節(jié))：n=3，l=40 mm，β=π，ξ=0.2，E=73 GPa；內外環(huán)柔性鉸鏈簧片尺寸L=46 mm，T=0.3mm，W=9.4mm；對比式 (12)、(14)，簡化前后彈簧的載荷位移關系和相對誤 差分別如圖10a、10b所示。

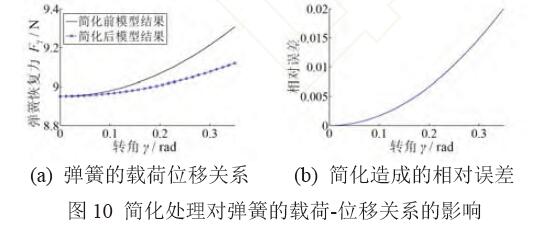
如圖10 所示，γ 小于0.35 rad(20°)時，簡化處 理對載荷位移曲線造成的相對誤差不超過2.0%，式

(13)的簡化處理可以用于構造零剛度柔性鉸鏈。

2.3 彈簧的剛度特性

設彈簧的剛度為K，聯(lián)立式(3)、(6)、(14)

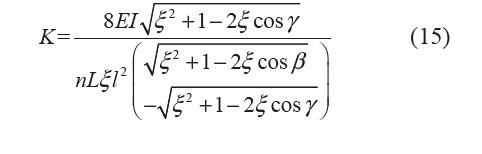
根據(jù)零剛度柔性鉸鏈實際加工參數(shù)(第4.2 節(jié))，彈簧剛度K 隨轉角γ的變化曲線如圖11所示。 特別地，當γ=0時，K 取得極小值。

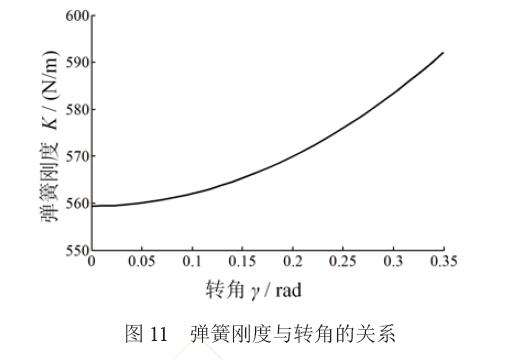
為便于設計和加工，彈簧采用線性正剛度彈簧，剛度為Kconst。整個行程內，零剛度柔性鉸鏈的總剛度大于等于零，則Kconst 應取K 的極小值

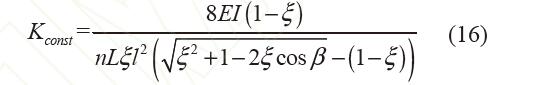
式(16)即為構造零剛度柔性鉸鏈時，線性正剛度彈簧的剛度取值。 2.4零剛度品質的分析 所構造的零剛度柔性鉸鏈載荷位移關系為

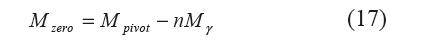
聯(lián)立式(2)，(8)、(16)可得

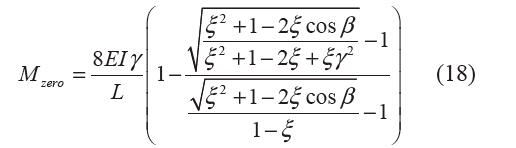
為評價零剛度的品質，定義添加負剛度模塊前后柔性鉸鏈剛度的降低幅度為零剛度品質系數(shù)η

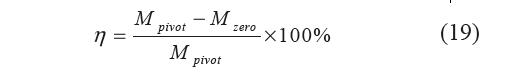
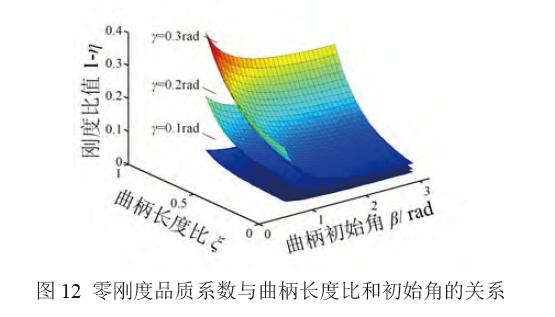
η 越接近100%，零剛度品質越高。圖12為1-η 與 曲柄長度比ξ 和初始角β 的關系。η 與曲柄彈簧機構并聯(lián)數(shù)n以及基座長度l 無關，僅與曲柄長度比ξ、轉角γ 以及初始角β 相關。

(1) 初始角β 增大，零剛度品質提高。

(2) 長度比ξ 增大，零剛度品質降低。

(3) 轉角γ 增大，零剛度品質降低。

為提高零剛度柔性鉸鏈的零剛度品質，初始角β應取較大的值；曲柄長度比ξ則應盡量小。同時根據(jù)第1.5 節(jié)的分析結果，ξ 過小，將導致曲柄彈簧機構提供負剛度的能力較弱。為提高零剛度柔性鉸 鏈的零剛度品質，選定：初始角β=π，曲柄長度比 ξ=0.2，即第4.2 節(jié)零剛度柔性鉸鏈的實際加工參數(shù)。

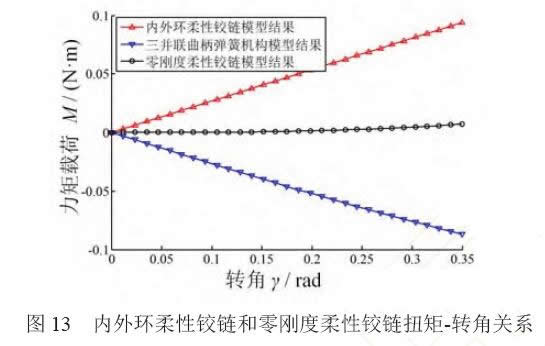
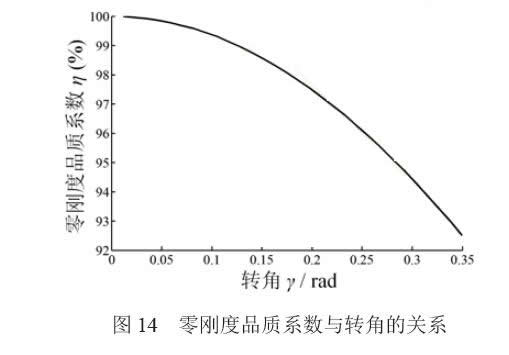
根據(jù)零剛度柔性鉸鏈的實際加工參數(shù)(第4.2 節(jié))，內外環(huán)柔性鉸鏈和零剛度柔性鉸鏈扭矩-轉角 關系如圖13所示；剛度降幅即零剛度品質系數(shù)η與轉角γ關系如圖14所示。由圖14：在0.35 rad(20°) 轉動范圍內，零剛度柔性鉸鏈的剛度平均降低了 97%；0.26 rad(15°)轉角時，降低了95%。

3 線性正剛度彈簧的設計

構造零剛度柔性鉸鏈通常是在柔性鉸鏈尺寸和剛度確定后，再反解出曲柄彈簧機構中彈簧的剛度， 因此對彈簧的剛度和尺寸要求都比較嚴格。另外， 初始角β=π，由圖5a，零剛度柔性鉸鏈轉動過程中， 彈簧一直處于壓縮狀態(tài)，即為“壓簧”。

傳統(tǒng)壓簧的剛度和尺寸難以精確定制，且應用時多需要導向機構。因此，提出一種剛度和尺寸可 以定制的彈簧——菱形片簧串。菱形片簧串(圖15) 由多個菱形片簧串聯(lián)構成，具有結構設計自由，定 制度高等特性，其加工工藝與柔性鉸鏈一致，均采 用精密線切割加工。

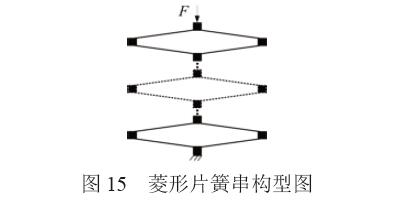
3.1 菱形片簧串的載荷-位移模型

由菱形片簧的對稱性，只需對一根簧片進行受 力分析，如圖16所示。 α 為簧片與水平之間的夾角，簧片的長寬厚分別為Ld、Wd、Td，f 為菱形片 簧所受的量綱一化載荷，δy 為菱形片簧在y 方向的 變形量，力fy 和力矩m 為等效在單個簧片末端上的載荷，fv 和fw 為fy 在wov 坐標系下的分力。

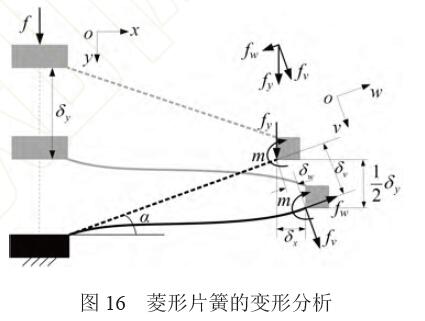
根據(jù)AWTAR[13]的梁變形理論，單簧片量綱一化的載荷位移關系式

由于剛體對簧片的約束關系，簧片在變形前后 末端轉角為零，即θ = 0。聯(lián)立式(20)～(22)

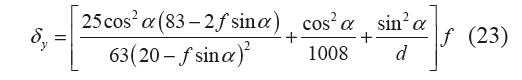
式(23)為菱形片簧的載荷-位移量綱一化模型。 n2 個菱形片簧串聯(lián)，其載荷-位移模型為

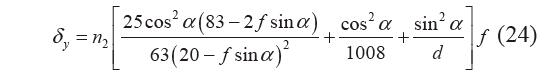
由式(24)，當αd 較小時，典型尺寸和典型載荷 下，菱形片簧串的剛度近似為線性剛度。

3.2 模型的有限元仿真驗證

對菱形片簧的載荷-位移模型進行有限元仿真 驗證。利用ANSYS Mechanical APDL 15.0，仿真參 數(shù)如表2 所示，對菱形片簧施加8 N 的壓力。

表2 菱形片簧串有限元仿真參數(shù)

參數(shù)	數(shù)值
材料	AL7075-T6
簧片長度Ld/mm	18
簧片寬度Wd/mm	10
簧片厚度Td/mm	0.25
簧片傾斜角α/°	10/20/30/40
彈性模量E/GPa	73

 

菱形片簧載荷位移關系的模型結果和仿真結果 對比如圖17 所示(量綱一化)。對四種不同傾斜角的 菱形片簧，模型與有限元仿真的結果相對誤差不超 過1.5%，式(24)模型的有效性和準確性得到驗證。

4 零剛度柔性鉸鏈的設計與試驗

4.1 零剛度柔性鉸鏈參數(shù)設計

設計零剛度柔性鉸鏈，首先應根據(jù)使用條件確 定柔性鉸鏈的設計參數(shù)，然后反算出曲柄彈簧機構 的相關參數(shù)。

4.1.1 柔性鉸鏈參數(shù)

內外環(huán)柔性鉸鏈交叉點位于簧片長度的 12.73%，其參數(shù)如表3 所示，代入式(2)，內外環(huán)柔 性鉸鏈的扭矩轉角關系為

表3 內外環(huán)柔性鉸鏈結構參數(shù)及材料屬性

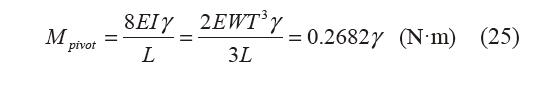
參數(shù)	數(shù)值
材料	AL7075-T6
簧片長度L/mm	46
簧片寬度W/mm	9.4
簧片厚度T/mm	0.30
彈性模量E/GPa	73

 

4.1.2 負剛度機構參數(shù)

如圖18 所示，取曲柄彈簧機構并聯(lián)數(shù)目n 為3， 由柔性鉸鏈的尺寸確定機座長度l=40 mm，根據(jù)第 2.4 節(jié)的結論，初始角β=π，曲柄長度比ξ=0.2。根 據(jù)式(16)反解出彈簧(即菱形片簧串)的剛度為 Kconst =558.81 N/m (26)

4.1.3 菱形片簧串參數(shù)

由l=40 mm，β=π，ξ=0.2，彈簧原長48 mm， 最大變形量(γ=0)為16 mm。由于結構限制，單個菱 形片簧難以產(chǎn)生這么大的變形，采用4 個菱形片簧 串聯(lián)(n2=4)，則單個菱形片簧的剛度為
Kd=4Kconst=2235.2 N/m (27)
根據(jù)負剛度機構的尺寸(圖18)，給定菱形片簧 的簧片長、寬和簧片傾斜角，由式(23)和菱形片簧 的剛度式(27)，可以反解出簧片厚度。菱形片簧結 構參數(shù)列于表4。

表4

綜上，基于曲柄彈簧機構的零剛度柔性鉸鏈的 參數(shù)已全部確定，如表3和表4所示。

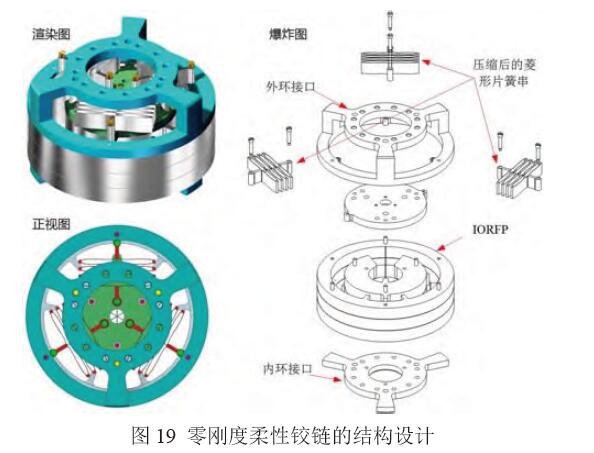
4.2 零剛度柔性鉸鏈樣件的設計與加工 參照文獻[8]對柔性鉸鏈的加工測試方法，零剛度柔性鉸鏈由負剛度機構和內外環(huán)柔性鉸鏈并聯(lián)而成，結構設計如圖19。

內外環(huán)柔性鉸鏈和菱形片簧串均采用精密線切 割機床加工，內外環(huán)柔性鉸鏈采用分層加工并裝配而成，圖20為三組菱形片簧串實物圖，圖21為裝 配完成的零剛度柔性鉸鏈樣件實物圖。

4.3 零剛度柔性鉸鏈的轉動剛度測試平臺 參照文獻[8]的轉動剛度測試方法，搭建零剛度 柔性鉸鏈的轉動剛度測試平臺，如圖22 所示。

4.4 試驗數(shù)據(jù)處理及誤差分析

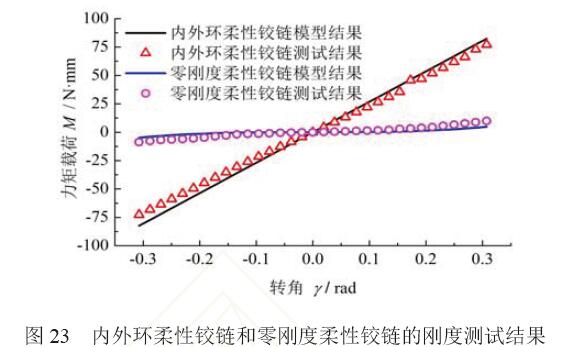
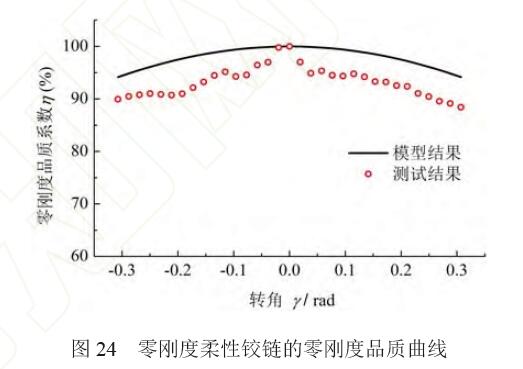
利用測試平臺對內外環(huán)柔性鉸鏈和零剛度柔性鉸鏈的轉動剛度進行測試，測試結果如圖23 所示。 根據(jù)式(19)計算并繪制零剛度柔性鉸鏈的零剛度品 質曲線，如圖24 所示。

測試結果表明：零剛度柔性鉸鏈的轉動剛度接近于零，相較于內外環(huán)柔性鉸鏈，零剛度柔性鉸鏈 在轉角±0.31 rad(18°) 剛度平均降低了93%； 0.26 rad (15°) 時，剛度降低了90%。

如圖23、24 所示，零剛度品質的測試結果和理論模型結果仍有一定差距(相對誤差小于15%)， 造成誤差的主要原因如下。

(1) 三角函數(shù)的簡化處理造成的模型誤差。

(2) 摩擦。菱形片簧串和安裝軸之間存在摩擦。

(3) 加工誤差。簧片實際尺寸存在誤差等。

(4) 裝配誤差。菱形片簧串安裝孔和轉軸之間的間隙，試驗平臺裝置的安裝間隙等。

4.5 與典型零剛度柔性鉸鏈的性能對比文獻[4]中利用交叉簧片柔性鉸鏈(Cross-axis flexural pivot, CAFP) 構造零剛度柔性鉸鏈 ZSFP_CAFP 如圖25 所示。

對比利用內外環(huán)柔性鉸鏈所構造的零剛度柔 性鉸鏈ZSFP_IORFP(圖21)與ZSFP_CAFP(圖25)

(1) ZSFP_IORFP，結構更加緊湊。

(2) ZSFP_IORFP 轉角范圍較小。轉角范圍受限 于柔性鉸鏈自身的轉角范圍；ZSFP_CAFP 轉角范 圍80°，ZSFP_IORFP 轉角范圍40°。

(3) ±18°的轉角范圍內，ZSFP_IORFP 零剛度品 質較高。ZSFP_CAFP 剛度平均降低87% ， ZSFP_IORFP 剛度平均降低93%。

5 結論

以純扭矩作用下的內外環(huán)柔性鉸鏈為正剛度 子系統(tǒng)，為構造零剛度柔性鉸鏈，完成了以下工作。

(1) 提出一種負剛度轉動機構——曲柄彈簧機 構，建立模型(式(6))分析了結構參數(shù)對其負剛度特 性的影響，給出了其負剛度特性的范圍(表1)。

(2) 通過匹配正負剛度，得到曲柄彈簧機構中 的彈簧的剛度特性(式(16))，建立模型(式(19))分析 了曲柄彈簧機構結構參數(shù)對零剛度柔性鉸鏈零剛度 品質的影響，理論上，在內外環(huán)柔性鉸鏈的可用行 程內(±20°)，剛度平均降低幅度可達97%。

(3)提出一種可定制剛度的“彈簧”——菱形 片簧串，建立其剛度模型(式(23))并進行了有限元驗 證。

(4) 完成了一種結構緊湊的零剛度柔性鉸鏈樣 件的設計、加工和測試。測試結果表明：純扭矩作 用下，在36°轉角范圍內，與內外環(huán)柔性鉸鏈相比， 零剛度柔性鉸鏈的剛度平均降低了93%。

所構造的零剛度柔性鉸鏈僅在純扭矩作用下，可 實現(xiàn)“零剛度”，未考慮承受復雜載荷條件的情況。 因此，復雜載荷條件下零剛度柔性鉸鏈的構造，是下 一步研究的重點。另外，降低零剛度柔性鉸鏈運動時 存在的摩擦是零剛度柔性鉸鏈的重要優(yōu)化方向。

參 考 文 獻

[1] HOWELL L L. Compliant Mechanisms[M]. New York: Johm Wiley&Sons, Inc, 2001.

[2] 于靖軍, 裴旭, 畢樹生, 等. 柔性鉸鏈機構設計方法的 研究進展[J]. 機械工程學報, 2010, 46(13):2-13. YU Jingjun, PEI Xu，BI Shusheng，et al. State-of-arts of Design Method for Flexure Mechanisms[J].Journal of Mechanical Engineering, 2010, 46(13):2-13.

[3] MORSCH F M, Herder J L. Design of a Generic Zero Stiffness Compliant Joint[C]// ASME International Design Engineering Conferences. 2010:427-435.

[4] MERRIAM E G, Howell L L. Non-dimensional approach for static balancing of rotational flexures[J]. Mechanism & Machine Theory, 2015, 84(84):90-98.

[5] HOETMER K, Woo G, Kim C, et al. Negative Stiffness Building Blocks for Statically Balanced Compliant Mechanisms: Design and Testing[J]. Journal of Mechanisms & Robotics, 2010, 2(4):041007.

[6] JENSEN B D, Howell L L. The modeling of cross-axis flexural pivots[J]. Mechanism and machine theory, 2002, 37(5):461-476.

[7] WITTRICK W H. The properties of crossed flexure pivots and the influence of the point at which the strips cross[J]. The Aeronautical Quarterly, 1951, II: 272-292.

[8] LIU L, Bi S, Yang Q, et al. Design and experiment of generalized triple-cross-spring flexure pivots applied to the ultra-precision instruments[J]. Review of Scientific Instruments, 2014, 85(10): 105102.

[9] 楊其資, 劉浪, 畢樹生,等. 廣義三交叉簧片柔性鉸鏈的旋轉剛度特性研究[J]. 機械工程學報, 2015, 51(13): 189-195.

YANG Qizi, LIU Lang, BI Shusheng, et al. Rotational Stiffness Characterization of Generalized Triple-cross-spring Flexure Pivots[J]. Journal of Mechanical Engineering, 2015, 51(13):189-195.

[10] Liu L, Zhao H, Bi S, et al. Research of Performance Comparison of Topology Structure of Cross-Spring Flexural Pivots[C]// ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, August 17–20, 2014, Buffalo, New York, USA. ASME, 2014 : V05AT08A025.

[11] LIU L, Bi S, Yang Q. Stiffness characteristics of inner–outer ring flexure pivots applied to the ultra-precision instruments[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science 1989-1996 (vols 203-210), 2017:095440621772172.

[12] SANCHEZ J A G. Criteria for the Static Balancing of Compliant Mechanisms[C]// ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, August 15–18, 2010, Montreal, Quebec, Canada. ASME, 2010:465-473.

[13] AWTAR S, Sen S. A generalized constraint model for two-dimensional beam flexures：Nonlinear strain energy formulation[J]. Journal of Mechanical Design, 2010, 132: 81009.

作者簡介：畢樹生(通信作者)，男，1966年出生，博士，教授，博士研究生導師。主要研究方向為全柔性機構及仿生機器人。