摘 要：柔性鉸鏈由于具有無間隙、無摩擦和易于一體化設(shè)計(jì)等諸多優(yōu)點(diǎn)，而被廣泛應(yīng)用于精密操作、機(jī)器人、微納定位等需要超精密高速運(yùn)動(dòng)的領(lǐng)域。面向高速高加速度雙側(cè)驅(qū)動(dòng)系統(tǒng)，針對(duì)運(yùn)動(dòng)系統(tǒng)的整體高剛度和局部相對(duì)低剛度特性，設(shè)計(jì)了一種具有平動(dòng)高剛度和扭轉(zhuǎn)低剛度的半輪型柔性鉸鏈。基于旋量變換理論，以半輪型柔性鉸鏈中柔性單元的尺寸和位置角度作為設(shè)計(jì)幾何參數(shù)，推導(dǎo)了鉸鏈的六自由度剛度矩陣模型，并綜合分析了各項(xiàng)設(shè)計(jì)幾何參數(shù)對(duì)鉸鏈的各向剛度、相對(duì)剛度以及轉(zhuǎn)動(dòng)誤差的影響，并以整體平動(dòng)高剛度和扭轉(zhuǎn)低剛度為設(shè)計(jì)約束條件，討論鉸鏈結(jié)構(gòu)參數(shù)的選取。結(jié)果表明：該設(shè)計(jì)方法更為簡(jiǎn)潔、快捷，從而為柔性鉸鏈的設(shè)計(jì)和應(yīng)用提供一定的依據(jù)。

0 引言

高速高加速度雙側(cè)驅(qū)動(dòng)系統(tǒng)在直線運(yùn)動(dòng)方向上具有高剛度，以保證高動(dòng)態(tài)特性下的高控制帶寬。同時(shí)，在扭轉(zhuǎn)方向上必須具有相對(duì)低剛度，以防止雙側(cè)驅(qū)動(dòng)力不一致造成同步誤差或扭轉(zhuǎn)而影響運(yùn)動(dòng)系統(tǒng)的穩(wěn)定性。柔性鉸鏈通常僅由一個(gè)部件構(gòu)成，按特殊需求對(duì)零件形狀進(jìn)行設(shè)計(jì)，使零件的某些特定區(qū)域特別薄弱，而在一些運(yùn)動(dòng)自由度上應(yīng)力應(yīng)變集中。再通過自身的柔性變形，來傳遞輸入端驅(qū)動(dòng)力和位移，從而獲得在固定坐標(biāo)系下的運(yùn)動(dòng)位移關(guān)系。正是由于這樣的特性，使得柔性鉸鏈適合應(yīng)用于高速運(yùn)動(dòng)系統(tǒng)中。

國內(nèi)外很多學(xué)者已對(duì)柔性鉸鏈作了大量研究，并取得了一定的成果。Smith等設(shè)計(jì)了橢圓型柔性鉸鏈，推導(dǎo)出橢圓型柔性鉸鏈柔度封閉方程，并利用有限元法和實(shí)驗(yàn)加以驗(yàn)證。Lobontiu等對(duì)各類缺口類型（包括角圓型、直圓型、橢圓型、拋物線型、雙曲線型、雙軸型、三段式、徑向?qū)ΨQ型）做了廣泛研究，建立了各種鉸鏈的閉環(huán)柔度方程，并分析了其精度和應(yīng)力等性能。Schot?borgh等[6]根據(jù)有限元仿真分析結(jié)果，并采用數(shù)值擬合法求得直圓型、直梁型和交叉型柔性鉸鏈的剛度及應(yīng)力的無量綱設(shè)計(jì)圖，從而幫助設(shè)計(jì)者在最初設(shè)計(jì)階段選擇柔性鉸鏈的類型和設(shè)計(jì)幾何參數(shù)。沈意平等[7]基于力插值的有限元法，建立了圓弧柔性鉸鏈的有限元分析模型，并推導(dǎo)出其一致質(zhì)量矩陣表達(dá)式。劉浪等[8]通過增加交叉簧片型柔性鉸鏈中的簧片數(shù)量，設(shè)計(jì)了一種一般化具有大運(yùn)動(dòng)行程的柔性鉸鏈。

本文針對(duì)上述問題提出了一種應(yīng)用于雙側(cè)驅(qū)動(dòng)系統(tǒng)的半輪型柔性鉸鏈設(shè)計(jì)方法。并基于旋量變換理論，建立了單個(gè)柔性鉸鏈和組合鉸鏈的剛度矩陣模型，以整體平動(dòng)高剛度和扭轉(zhuǎn)低剛度為設(shè)計(jì)約束條件，綜合分析了各項(xiàng)設(shè)計(jì)幾何參數(shù)對(duì)鉸鏈的各向剛度、相對(duì)剛度以及轉(zhuǎn)動(dòng)誤差3個(gè)性能指標(biāo)的影響。通過有限元仿真分析，驗(yàn)證模型的有效性。

1 半輪型柔性鉸鏈設(shè)計(jì)

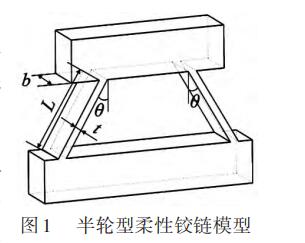
為了滿足雙側(cè)驅(qū)動(dòng)系統(tǒng)自由度的剛度需求，本文采用一種半輪型柔性鉸鏈如圖1所示，可實(shí)現(xiàn)系統(tǒng)在X、Y自由度具有高剛度以及Rz自由度具有相對(duì)較低剛度。其中，L為梁的長(zhǎng)度，b為梁的寬度，t為梁的厚度，θ為兩側(cè)子柔性單元與整個(gè)鉸鏈端面法線間夾角。該半輪型柔性鉸鏈兩側(cè)對(duì)稱設(shè)有兩個(gè)均勻直梁型子柔性單元結(jié)構(gòu)，實(shí)現(xiàn)吸收運(yùn)動(dòng)件在Rz自由度上產(chǎn)生的順時(shí)針或逆時(shí)針方向的扭轉(zhuǎn)。

2 鉸鏈剛度矩陣模型的建立

半輪型柔性鉸鏈上設(shè)有橫截面積為矩形的均勻直梁型柔性單元，使其一端固定，在自由端建立如圖2所示坐標(biāo)系。

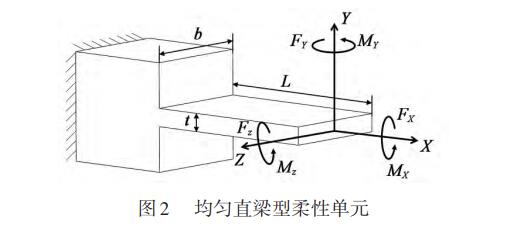
柔性鉸鏈在自由端上承受力旋量F=[FX,FY,FZ,MX,MY,MZ]T，對(duì)應(yīng)方向產(chǎn)生的微小形變旋量為ζ=[δX,δY,δZ,θX,θY,θZ]T，其中{FX,FY,FZ}T為沿對(duì)應(yīng)坐標(biāo)軸的力，{MX,MY,MZ}T為繞對(duì)應(yīng)坐標(biāo)軸的力矩，{δX,δY,δZ}T為沿對(duì)應(yīng)坐標(biāo)軸的伸縮形變量，{θX,θY,θZ}T為繞對(duì)應(yīng)坐標(biāo)軸的扭轉(zhuǎn)和彎曲角度。

根據(jù)胡克定理，F(xiàn)=Kζ，梁的六自由度剛度矩陣可表示為:

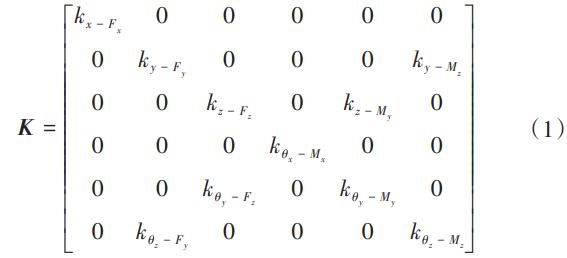
根據(jù)Timoshenko梁理論模型，剛度矩陣K中元素方程可表示為：

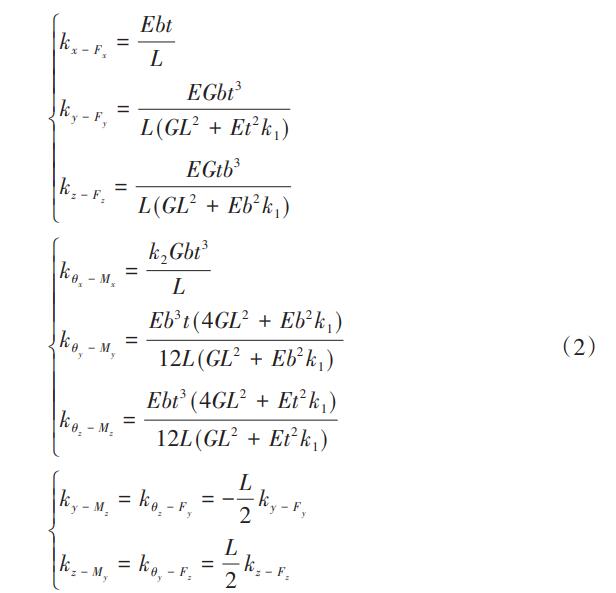
式中：E為楊氏模量；G為剪切模量；k1為剪切修正系數(shù)，對(duì)于矩形截面k1=6/5;k2為矩形截面自由扭轉(zhuǎn)時(shí)的抗扭截面系數(shù)的因數(shù)，其取值為“橫截面長(zhǎng)/寬”相關(guān)的因數(shù)。

如圖3所示，建立兩個(gè)子柔性單元1、2的局部坐標(biāo)系，使兩個(gè)局部坐標(biāo)系的原點(diǎn)分別與其對(duì)應(yīng)單元橫截面的形心重合。

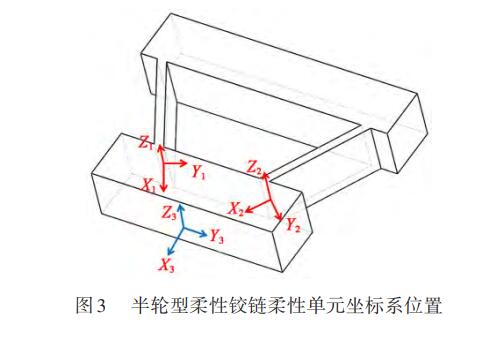
在該半輪型柔性鉸鏈中，子柔性單元1、2形成并聯(lián)結(jié)構(gòu)。在同一坐標(biāo)系中，其末端剛度為各并聯(lián)單元的剛度之和。為計(jì)算半輪型柔性鉸鏈對(duì)雙側(cè)驅(qū)動(dòng)系統(tǒng)在各方向的支撐剛度，各單元的剛度矩陣應(yīng)整合至坐標(biāo)系{O3,X3,Y3,Z3}中。

本文設(shè)置各子柔性單元的尺寸參數(shù)如表1所示，其中已知參數(shù)由具體功能、材料（兩側(cè)的均勻直梁型子柔性單元結(jié)構(gòu)均采用彈簧鋼60Si2Mn）所確定，未知參數(shù)為本文所研究的影響鉸鏈性能的相關(guān)參數(shù)。

將上述數(shù)值和參數(shù)代入剛度矩陣（1）、（2），并計(jì)算可得到各子柔性單元（1、2）關(guān)于其各自局部坐標(biāo)系的剛度矩陣K1(1）、K2(2）分別為：

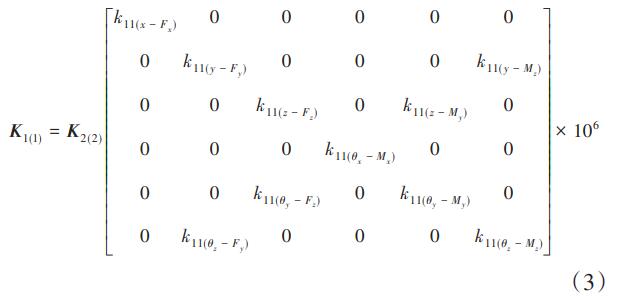
根據(jù)余靖軍提出的理論，剛度矩陣和柔度矩陣的旋量坐標(biāo)變換式為：

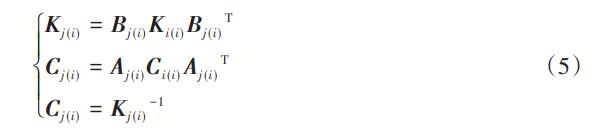
式中：A、B為旋量伴隨變換矩陣，滿足上述式中A-1=BT;j (i)為坐標(biāo)系{oi}中的剛度矩陣關(guān)于坐標(biāo)系{oj}的表達(dá)。

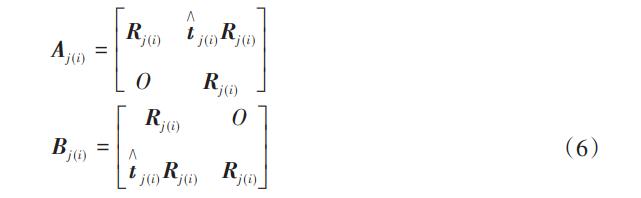
式中：Rj (i)為坐標(biāo)系{oi}關(guān)于{oj}的方向余弦矩陣，其變量為繞Z坐標(biāo)軸的旋轉(zhuǎn)角度γj (i);t j (i)為坐標(biāo)系{oi}關(guān)于{oj}的反對(duì)稱移動(dòng)矩陣，其變量為沿X、Y和Z坐標(biāo)軸的平動(dòng)量，即（xj (i),yj(i),zj(i)):

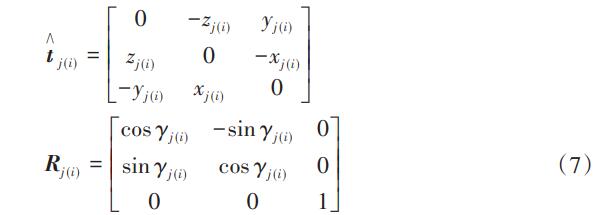
綜上，半輪型柔性鉸鏈中各子柔性單元?jiǎng)偠染仃囋谀┒俗鴺?biāo)系{O3,X3,Y3,Z3}中的整合總剛度矩陣為：

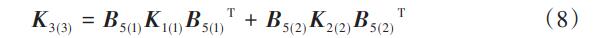
3 鉸鏈性能分析

柔性鉸鏈?zhǔn)且环N利用自身材料的柔性變形傳遞作用力和形變的機(jī)械連接部件。本文針對(duì)該半輪型柔性鉸鏈的性能分析，選擇鉸鏈的各向剛度、相對(duì)剛度以及轉(zhuǎn)動(dòng)誤差3項(xiàng)指標(biāo)進(jìn)行研究。以未知參數(shù)包括鉸鏈兩側(cè)對(duì)稱設(shè)置的子柔性單元的長(zhǎng)度L1、厚度t1以及其設(shè)置位置與端面法線夾角θ為控制變量，通過數(shù)值仿真可以得到這些參數(shù)（L1,t1,θ）對(duì)半輪型柔性鉸鏈各項(xiàng)性能的影響，為半輪型柔性鉸鏈最優(yōu)結(jié)構(gòu)參數(shù)選取提供指導(dǎo)。

3.1 各向剛度

剛度表示柔性鉸鏈在受力時(shí)不同方向上抵抗彈性變形的能力，從數(shù)值上體現(xiàn)柔性鉸鏈彈性變形的難易程度。半輪型柔型鉸鏈變形發(fā)生在繞Z軸轉(zhuǎn)動(dòng)的Rz方向上。然而在對(duì)于雙側(cè)驅(qū)動(dòng)系統(tǒng)，柔性鉸鏈通常會(huì)在多個(gè)方向受力導(dǎo)致發(fā)生形變。因此，為了滿足雙側(cè)驅(qū)動(dòng)系統(tǒng)的X、Y方向高剛度要求以及Rz方向的低剛度要求，有必要綜合研究半輪型柔性鉸鏈在X、Y和Rz自由度上的剛度。

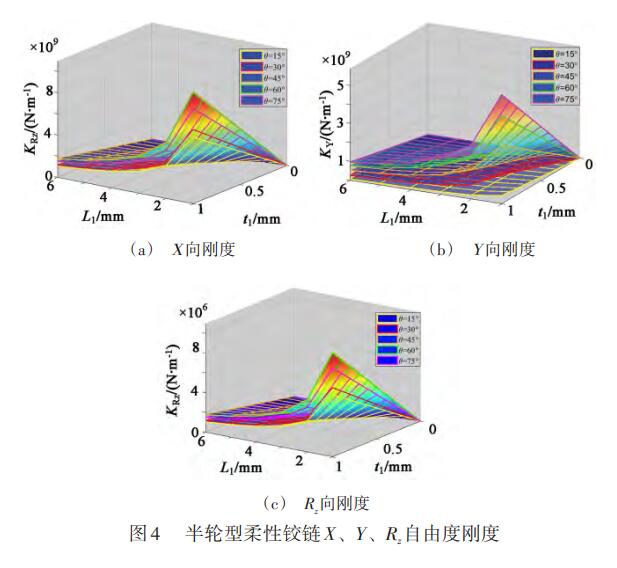
控制參數(shù)點(diǎn)坐標(biāo)（L1,t1）與子柔性單元位置角度θ對(duì)半輪型柔性鉸鏈X、Y和Rz自由度的剛度影響如圖4所示。由圖可以看出，在位置角度θ一定的情況下，變量L1越小，即梁的長(zhǎng)度越短，半輪型柔性鉸鏈3個(gè)自由度上的剛度越大；變量t1越大，即梁的厚度越厚，半輪型柔性鉸鏈各自由度的剛度越大。當(dāng)位置角度由15°變化到75°的過程中，半輪型柔性鉸鏈X自由度剛度與Y自由度剛度受梁的厚度及長(zhǎng)度的影響情況呈現(xiàn)對(duì)調(diào)趨勢(shì)，且在θ=45°時(shí)其X自由度剛度等于Y自由度剛度。另外，在θ=45°的情況下，梁的厚度及長(zhǎng)度對(duì)半輪型柔性鉸鏈Rz自由度剛度影響最明顯。

3.2 相對(duì)剛度

期望所設(shè)計(jì)柔性鉸鏈在一定方向上產(chǎn)生變形，這一變形方向稱之為工作方向，則其他方向就是非工作方向。由于非工作方向上的剛度并非無窮大，因此柔性鉸鏈在一定載荷下工作時(shí)，非工作方向會(huì)產(chǎn)生一定程度的變形位移，稱之為寄生位移。因此，定義相對(duì)剛度為工作方向上剛度與非工作方向上剛度的比值。

對(duì)于半輪型柔性鉸鏈，工作方向?yàn)槔@Z軸轉(zhuǎn)動(dòng)的Rz方向，X、Y方向則為非工作方向。施加的載荷主要為繞Z軸的轉(zhuǎn)矩Mz和xOy平面內(nèi)的力，所以半輪柔性鉸鏈發(fā)生的變形和寄生位移均發(fā)生在xOy平面內(nèi)，因此本節(jié)只需考慮xOy平面內(nèi)的相對(duì)剛度。將剛度矩陣（10）中可得半輪型柔性鉸鏈相對(duì)剛度Ratio1、Ratio2為：

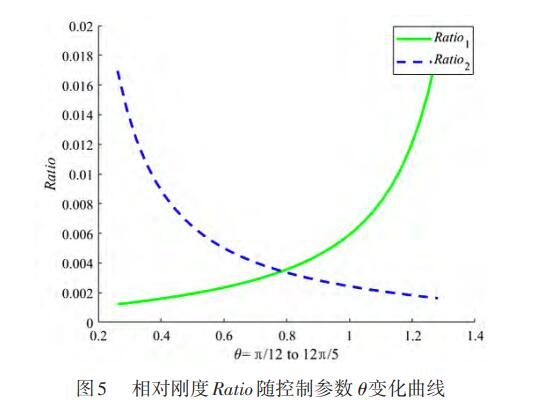
θ對(duì)Ratio1、Ratio2的影響如圖5所示。由圖可以看出，Ratio1的值隨θ的增大而增大且在階段變化顯著；相反地，Ratio2的值隨θ的增大而減小且在變化顯著，但兩條變化曲線是非對(duì)稱的。且在θ=45°的情況下，Ratio1=Ratio2。

3.3 轉(zhuǎn)動(dòng)誤差

高精度是柔性鉸鏈與傳統(tǒng)剛性鉸鏈相比的一個(gè)顯著優(yōu)點(diǎn)。理想的剛性鉸鏈假設(shè)存在一個(gè)理想的轉(zhuǎn)動(dòng)軸或基點(diǎn)，鉸鏈的運(yùn)動(dòng)部分圍繞轉(zhuǎn)動(dòng)軸或基點(diǎn)轉(zhuǎn)動(dòng)。然而在實(shí)際應(yīng)用中剛性鉸鏈存在裝配間隙，實(shí)際的轉(zhuǎn)動(dòng)軸或基點(diǎn)與理想位置存在一定偏差。柔性鉸鏈由于僅由一個(gè)部件加工而成，不存在裝配間隙，但是柔性鉸鏈在一定載荷作用下發(fā)現(xiàn)變形時(shí)，其自由端理想情況下會(huì)產(chǎn)生一個(gè)圓弧彎曲，并且這個(gè)圓弧的圓心相對(duì)于鉸鏈應(yīng)該是固定不變的。然而在實(shí)際應(yīng)用中，圓弧的曲率和圓心的位置都會(huì)與理想情況產(chǎn)生一定程度的偏差。

柔性鉸鏈的轉(zhuǎn)動(dòng)誤差定義為變形后的基點(diǎn)位置p'與初始位置之間的距離。轉(zhuǎn)動(dòng)誤差定量描述柔性鉸鏈變形時(shí)虛擬轉(zhuǎn)動(dòng)軸或基點(diǎn)的移動(dòng)情況，轉(zhuǎn)動(dòng)誤差越小，柔性鉸鏈的精度越高。因此，根據(jù)等效柔性鉸鏈模型中初始基點(diǎn)位置，以端面中心為原點(diǎn)建立三維坐標(biāo)系，分析其轉(zhuǎn)動(dòng)誤差，如圖6所示。從而等效分析半輪型柔性鉸鏈的精度。

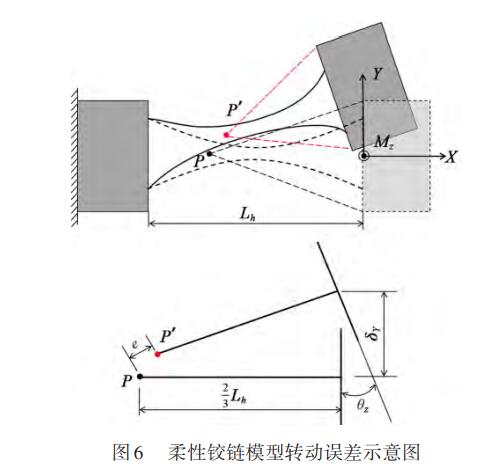
整體半輪型柔性鉸鏈的長(zhǎng)度為L(zhǎng)h，在力矩MZ的作用下，通過幾何關(guān)系計(jì)算轉(zhuǎn)動(dòng)誤差e可表示為：

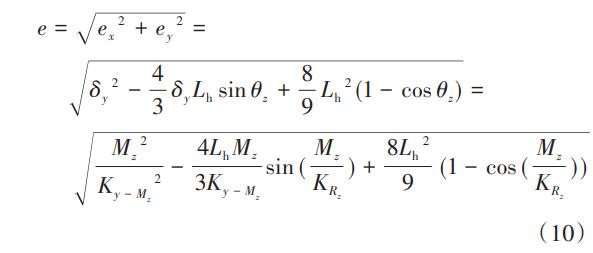
提取半輪型柔性鉸鏈總剛度矩陣（8）中對(duì)應(yīng)位置剛度，并代入式（10），得到控制參數(shù)點(diǎn)坐標(biāo)（L1,t1）與子柔性單元位置狀態(tài)量角度θ對(duì)半輪型柔性鉸鏈轉(zhuǎn)動(dòng)誤差影響如圖7所示。從圖中可以看出，在位置角度θ一定的情況下，變量L1越大，即梁的長(zhǎng)度越長(zhǎng)，半輪型柔性鉸鏈轉(zhuǎn)動(dòng)誤差e越大；變量t1越小，即梁的厚度越薄，半輪型柔性鉸鏈轉(zhuǎn)動(dòng)誤差e越大。軸轉(zhuǎn)動(dòng)誤差e隨θ的增大而減小，并且在15°～30°變化明顯，在45°～75°變化將不再明顯。

通過上述分析，為了滿足半輪型柔性鉸鏈X方向和Y方向高剛度需求需選取合適的L1和t1，但兩相對(duì)剛度呈現(xiàn)對(duì)調(diào)趨勢(shì)，即實(shí)現(xiàn)一個(gè)方向的高剛度而另一方向卻呈現(xiàn)低剛度。同樣地，兩相對(duì)剛度Ratio1、Ratio2隨θ的增大也呈現(xiàn)相反變化趨勢(shì)。所以針對(duì)位置角度θ的選取，選取θ=45°，即兩側(cè)子柔性單元與整個(gè)鉸鏈端面法線間夾角為45°。此時(shí)，半輪型柔性鉸鏈的X自由度剛度和Y自由度剛度變化趨勢(shì)相同，可方便通過選取合適的L1和t1實(shí)現(xiàn)兩方向高剛度的要求，且轉(zhuǎn)動(dòng)誤差也相對(duì)很小。

4 結(jié)束語

本文針對(duì)雙側(cè)驅(qū)動(dòng)系統(tǒng)的整體高剛度和局部相對(duì)低剛度特性，研究了一種半輪型柔性鉸鏈結(jié)構(gòu)的設(shè)計(jì)方法。基于旋量變換理論，以半輪型柔性鉸鏈中子柔性單元的長(zhǎng)度L1、厚度t1以及位置角度θ作為參數(shù)，建立半輪型柔性鉸鏈的剛度矩陣模型。提取剛度矩陣中X、Y、Rz自由度剛度對(duì)應(yīng)的元素，通過分析半輪型柔性鉸鏈的各向剛度和相對(duì)剛度，表明在設(shè)計(jì)計(jì)算時(shí)應(yīng)優(yōu)先考慮θ，這樣鉸鏈的剛度性能分析就轉(zhuǎn)換為選取合適的L1和t1實(shí)現(xiàn)兩方向高剛度的要求，為柔性鉸鏈的結(jié)構(gòu)設(shè)計(jì)提供理論依據(jù)。

第一作者簡(jiǎn)介：胡金鑫 （1996-），男，碩士，研究實(shí)習(xí)員，研 究領(lǐng)域?yàn)闄C(jī)器人動(dòng)力學(xué)與運(yùn)動(dòng)控制，已發(fā)表論文2篇。

通訊作者簡(jiǎn)介：韓哈斯敖其爾 （1986-），男，博士，副研究 員，研究領(lǐng)域?yàn)榭臻g機(jī)構(gòu)設(shè)計(jì)、并聯(lián)機(jī)構(gòu)運(yùn)動(dòng)學(xué)分析。